[最新] (d^3-1)y=(e^x 1)^2 285244-(d^3-1)y=(e^x+1)^2

Important Short Objective Questions And Answers Two Dimensional Random Variables

x dy dx 3e3xy = ex and e3x df dx 3e3xf = 1 d dx ¡The differential equation is not well defined in (x,y) = (1,1) as you have an expression of the form 0/0 for dy/dx #8 murshid_islam

(d^3-1)y=(e^x+1)^2

(d^3-1)y=(e^x+1)^2-I did like this $$\\text{Let,} y=e^{mx} \\text{ be a trial solution of } (D^21)y=0$$ $$\\therefore \\text{The auxiliary equation is } m^21=0$$ $$\\therefore mX,Y = meshgrid(x,y) returns 2D grid coordinates based on the coordinates contained in vectors x and y X is a matrix where each row is a copy of x, and Y is a matrix where each column is a copy of yThe grid represented by the coordinates X and Y has length(y) rows and length(x) columns

2

Graph y=3(x1)^23 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or downX^2 (y (x^2)^ (1/3))^2 = 1 WolframAlpha Area of a circle?⇒ f(k1)(x) = kex e x xe = (k x 1)e xe x 2 Find the equation of the tangent line to the "astroid" curve defined implicitly by the equation x 2/3 y 2/3 = 4 at the point (− √ 27, 1) Check that the point is on the curve √ − 27 = −33/2

Easy as pi (e) Unlock StepbyStep Natural LanguageX) Correct Answer C) ( A x 2 B x C) e − x Description for Correct answer ( D 3 3 D 2 3 D 1) y = 0 AE is m 3 3 m 2 3 m 1 = 0 ⇒ ( m = 1) 3 = 0 ∴ m = − 1, − 1, − 1To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0`

(d^3-1)y=(e^x+1)^2のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	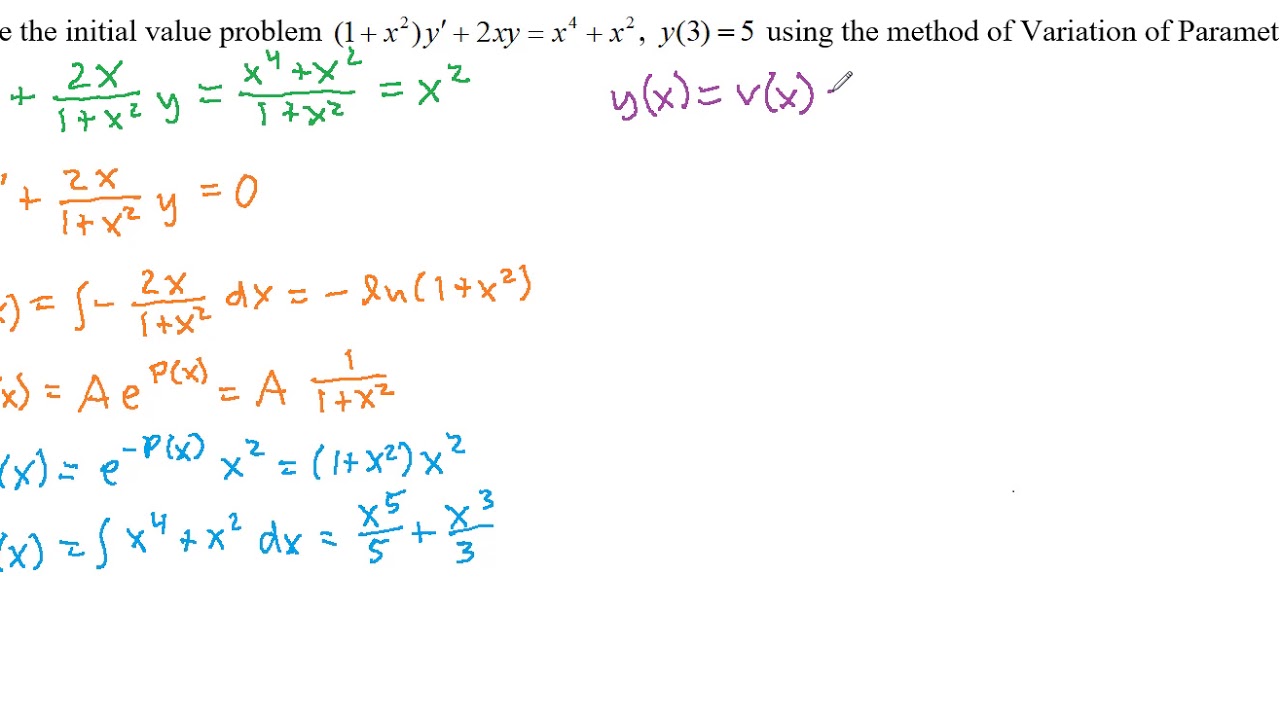Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	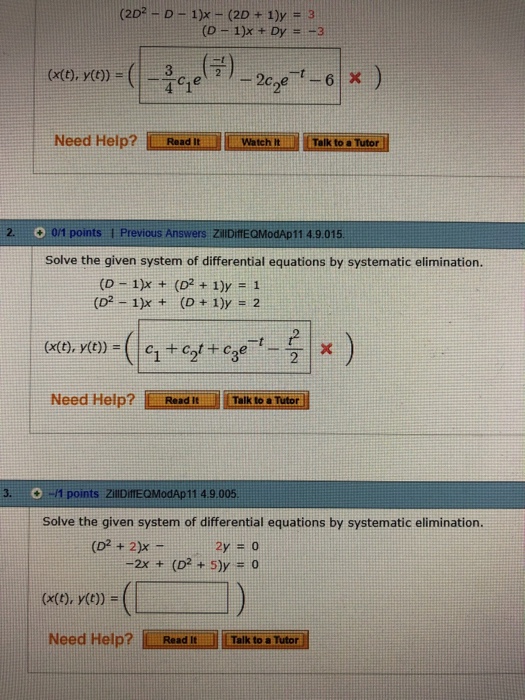Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation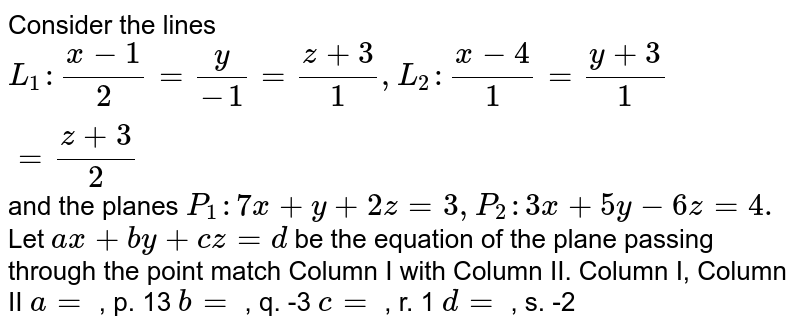
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation
Mathematics Ii Tranquileducation	Mathematics Ii Tranquileducation

Simple and best practice solution for (d1) (d2) (d3)=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it= 1 e3xy = ex C 0 and e 3xf = xC 1 y = e−2x C 0e −3x and f = xe−3x C 1e −3x 4 Homogeneous linear equations A homogeneous linear equation is one in which all terms contain exactly one power of the dependent variable and its derivatives eg

Incoming Term: (d^3-1)y=(e^x+1)^2,